Kako daleč lahko vidite meteor?
>Dobim e -pošto.
skript za manifest
Večina postavlja različne vrste vprašanj, od katerih je večina precej preprosta za odgovoriti (pravzaprav bi na veliko lahko odgovorili z googlanjem, namigom). Včasih pa dobim vprašanje, na katerega je težje odgovoriti, ali celo vprašanje, o katerem sem se spraševal o sebi, a ga nisem mogel ugotoviti.
Tako sem bil zelo zaintrigiran, ko sem od Bad Readerja Deana Lewisa vprašal o meteorjih. Med meteorskim dežjem Perzeid leta 2018 je bil odsoten od svoje družine, ločeno s približno 1000 kilometri. Če bi videl meteor, ali je bilo mogoče videti istega meteorja z njihove oddaljene lokacije?
Kratek odgovor je: Da! Dolg odgovor je ... matematika. Kul, zabavna matematika.
In ko vidim, kako bo ob objavi tega članka nocoj dosežen vrhunec letne meteorske plohe Geminid leta 2018, se mi zdi primerno to ugotoviti.
Astronomija tečaja nesreče: meteorji, meteoroidi in meteoriti, o moj!
Če bi bila Zemlja popolnoma ravna, bi načeloma lahko videli meteor vse do katerega koli roba Zemlje. Dokler ste nad tlemi, tudi majhni, potem vaša vidna linija doseže vsak kvadratni centimeter planeta na vaši strani, zato je vsak meteor viden vsem. V resnici zrak ni popolnoma prozoren, zato na neki razdalji gledate skozi toliko blata, da ne vidite ničesar.
Vendar pa Zemlja ni ravna. Resno! Okrogla je. In ozračje ga obdaja kot lupina, ki se z višino tanjša in sčasoma odstrani; ta višina je odvisna od vaše definicije prostora. Lahko pa malce goljufamo, saj poznamo znanost: meteorji, kot so tisti pod prho, ponavadi izgorijo približno 100 kilometrov nad tlemi. Ta višina je odvisna od mnogih stvari, tudi od tega, kako velika je meteoroidi (trdni delci medplanetarnih naplavin, ki drsejo skozi vesolje) so, kako hitro se premikajo, pod kakšnim kotom vstopajo v ozračje itd. Ampak recimo temu 100 km.
Najbližji meteor vam je lahko, če ste neposredno pod njim, potem pa je 100 km naravnost navzgor (v vašem zenitu). Če izgori dlje od zenita, potem mora biti dlje od vas. Najbolj oddaljeno od meteorja, je razumljivo, če je točno na obzorju.
Geometrija je videti tako (opomba: NE za merjenje):
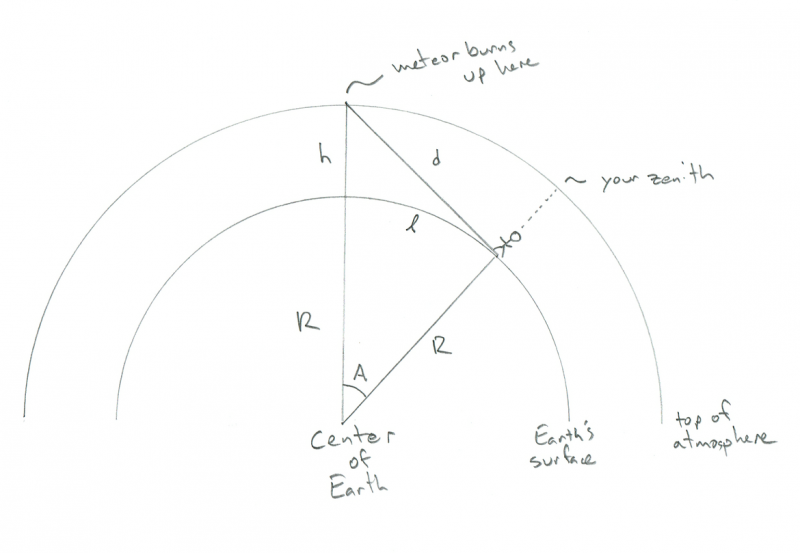
Shema, ki prikazuje geometrijo opazovalca, ki opazuje goreč meteor. Zasluge: Phil Plait
Ogledate si lahko majhnega človeka, ki stoji na površini ukrivljene Zemlje - recimo to ste vi - z (tudi ukrivljenim) ozračjem nad njimi. V tem diagramu je R polmer Zemlje (6.4000 km), h je višina, do katere meteor izgori (100 km), d pa je razdalja od vas do meteorja. A je kot med vašim položajem na Zemlji in položajem meteorja nad njo, kurziv l (po dolžini) pa je razdalja, ki bi jo morali prehoditi, da bi bil meteor neposredno nad glavo (vem, da se to zdi čudno želeti vedeti, vendar zdrži z mano). Čudno, tukaj lahko izračunate vse, kar potrebujete, ne da bi vedeli d, ampak no, kul je vedeti, kako daleč je meteor, kajne?
Ključ do vsega tega je, da je kot med meteorjem, vami in središčem Zemlje pravi kot. To je zato, ker je meteor na obzorju, kot ga vidite (ali, če imate raje zabaven žargon, na tangentni črti v notranjem krogu, kjer ga R seka). Zaradi tega je trikotnik pravokoten trikotnik, in če se spomnite gimnazijske matematike, to pomeni, da lahko najdete vse stranice in kote!
Zapomni si Pitagorin izrek ? V pravokotnem trikotniku je kvadrat dolžine hipotenuze enak vsoti kvadratov drugih dveh strani*. V našem trikotniku je hipotenuza R+h, ostale stranice pa R in d.
Torej
(R+h)2= d2+ R2
ali pomnožite levo stran (uporabite FOLIJA ):
R2+ 2Rh + h2 = d2+ R2
Rešite za d, da vidite, kako daleč je meteor od vas. Upoštevajte, da je R2 na obeh straneh, zato jih prekličite
d2= 2Rh + h2
Or
d = kvadratni koren (2Rh + h2)
No, vse te številke poznamo! Plug-n-chug, baby:
d = kvadratni koren (2 x 6.400 x 100 + 10.000) = 1.136 km
Aha! To pomeni, da če na obzorju vidite meteor, je oddaljen več kot 1.100 kilometrov! To je daleč in tehnično najbolj oddaljeno lahko vidite meteor od tal.
Zdaj pa poiščimo kurziv l. Najprej moramo poznati kot A. To zahteva nekaj trigonometrije. Tam je veliko trig identitete lahko uporabite, da to ugotovite, vendar moj najljubši†je, da je v pravokotnem trikotniku sinus kota dolžina nasprotne strani, deljena z dolžino hipotenuze. Torej, če dobimo to razmerje, lahko vzamemo inverzni sinus (ali arcsin), da dobimo kot.
sin (A) = d / (R + h)
tarot vodnik visoke svečenice
torej
A = brez-1(d / R + h)
Spet priklopi-n-chug in dobim A = 10 °. To je spodoben kos zemeljske površine!
In zdaj lahko dobimo kurziv l. Okoli Zemlje je 360 °, obseg Zemlje pa je 2 x pi x polmer = 40.192 km, zato
40.192 km / 360 ° = 112 kilometrov na stopinjo
kar pomeni 10 ° = 1.120 kilometrov. To je precej blizu d, kar ni preveč presenetljivo. Risbe so pretirane, v resnici pa je lupina zraka nad nami majhna v primerjavi z velikostjo Zemlje. Če bi risbe prilagodili, bi videli, da sta d in l res zelo blizu po dolžini.
V redu, zakaj sem tako vroča in se trudim, da bi našla l? Zaradi prvotnega vprašanja! Če ste po vsej tej matematiki pozabili, kako daleč sta lahko dve osebi in še vedno vidita isti meteor?
No, v tem primeru bi bil meteor neposredno med njima in na vsakem njihovem obzorju. Geometrija izgleda takole:
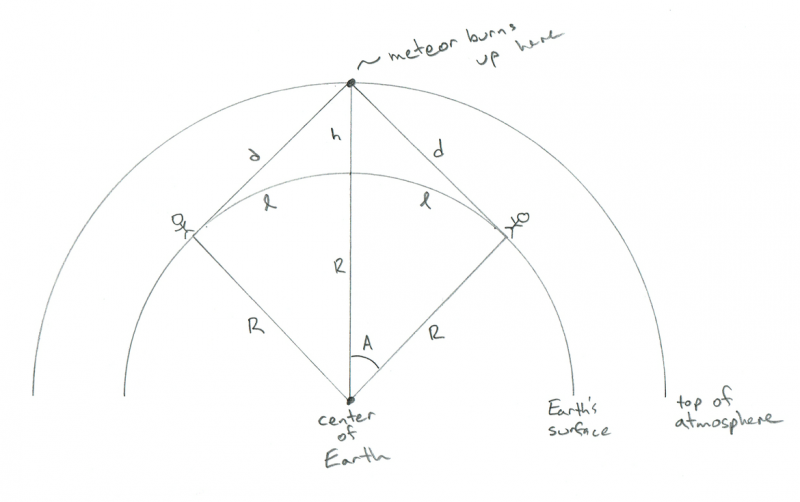
Shema, ki prikazuje geometrijo dveh opazovalcev, ki opazujeta meteor, ki gori med njima. Zasluge: Phil Plait
AHA! Zdaj vidite, zakaj si želim! Razdalja med dvema osebama je le 2 x l! Torej imamo odgovor:
Če dve osebi vidita isti meteor, nista na razdalji največ 2 x 1.120 = 2.240 kilometrov narazen. Na primer, to je precej blizu razdalje med Washingtonom in Denverjem. Vau.
Mimogrede, za spremembo perspektive (dobesedno) to pomeni z vidika meteorja, da lahko vidi odsek Zemlje širok 2.240 kilometrov (kot v DC na vzhodnem delu Zemlje in Denver na zahodnem). To je zelo kul.
In to nas pripelje do dejanskega odgovora na Deanovo vprašanje: Če je bil 1000 km od svoje družine, potem ja, tehnično bi lahko videli isti meteor. Kaj pa to?
To spet predpostavlja, da je zrak popolnoma čist in vse to, kar je v resnici v bistvu nemogoče. Torej ta matematika predstavlja idealno situacijo (vključno z idejo, da je meteor točno med njima).
Bodimo bolj realni. Recimo, da meteor za oba opazovalca izgori na nebu na nadmorski višini 45 ° nad obzorjem. Kako daleč bi bili drug od drugega? No, spet ob predpostavki, da je meteor točno med njima, je geometrija bolj takšna:
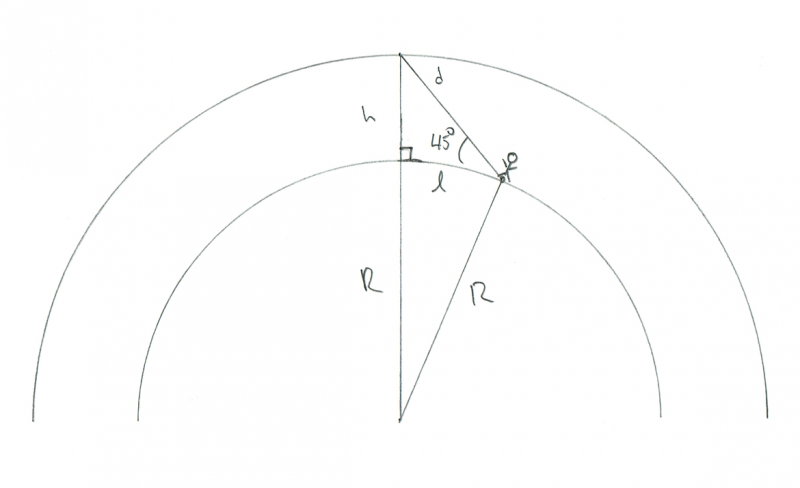
Shema, ki prikazuje geometrijo opazovalca, ki gleda meteor, ki gori 45 ° nad obzorjem. Zasluge: Phil Plait
To je pravzaprav težje rešiti, vendar poznam še en trik: če predpostavimo, da je l majhen, ukrivljenost Zemlje ne bo pomembna. Na primer, če želim vedeti razdaljo med dvema drevesoma na svojem dvorišču, mi je vseeno, da je Zemlja ukrivljena. Na tako majhni razdalji lahko domnevam, da je ravna. Naredimo to predpostavko tukaj.
V tem primeru imamo še en pravokotni trikotnik, vendar je tokrat pravi kot tisti pod meteorjem. V diagramu sem ga celo označil z majhno kvadratno oznako. Torej, če je to kot 90 ° in je naš kot do meteorja 45 °, potem je zadnji kot (od meteorja do opazovalca) tudi 45 °. To pomeni, da mora biti to enakokraki trikotnik, zato sta l in h enaka! Ker vemo, da je h 100 km, mora tudi l.
In to pomeni, da je razdalja med našima opazovalcema dvakrat večja ali 200 km.
Mimogrede, v tem primeru je razdalja do meteorja približno 141 km. Bralcu bom to potrdil kot vajo.
Načeloma to pomeni, da če veste, kako visoko je meteor od obzorja, in nadmorsko višino, na kateri je zgorel, lahko izračunate njegovo razdaljo (ali če poznate razdaljo, lahko dobite njeno višino). Ta sprožilec je sicer precej zapleten in mislim, da sem za danes namenil dovolj matematike.
Ampak kul je misliti, da ima lahko malo srednješolske matematike tako zabavno aplikacijo. Priznam, da je poetično in romantično vedeti, da je mogoče, če ločitev ni predaleč, videti, da vidiš padajočo zvezdo z nekom drugim. Kako ljubka misel.
* V Čarovnik iz Oza , strašilo se je zmotilo po ima možgane.
† Od seveda Imam najljubšo identiteto trig. Kaj je tvoje?













